Maching learning in action，决策树(decision tree)ID3算法笔记

发表于   |   分类于   |  

决策树(decision tree)

决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程,它可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布.

决策树的构造

常用的算法是ID3, C4.5和CART算法.这里使用ID3算法

信息增益

在划分数据集之前之后信息发生的变化称为信息增益.信息增益最高的特征为最好的选择.ID3算法使用信息增益信息构造决策树,C4.5使用信息增益比.

计算香农熵(简称熵)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from math import log
def calShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts:
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob, 2)
    return shannonEnt

数据集

1
2
3
4
5
6
7
8
def createDataSet():
    dataSet = [[1, 1, 'yes'],
              [1, 1, 'yes'],
              [1, 0, 'no'],
              [0, 1, 'no'],
              [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return dataSet, labels
1
2
myDat, labels = createDataSet()
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

1
calShannonEnt(myDat)
0.9709505944546686

1
2
myDat[0][-1] = 'maybe'
myDat
[[1, 1, 'maybe'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

1
calShannonEnt(myDat)
1.3709505944546687

划分数据集

按照给定特征划分数据集

1
2
3
4
5
6
7
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            retDataSet.append(featVec[:axis]+featVec[axis+1:])
#     print retDataSet
    return retDataSet

这里使用的是retDataSet.append(featVec[:]),简化了书中的代码.

Python语言不考虑内存分配的问题,Python语言在函数中传递的是列表的引用,在函数内部修改对列表的引用,将会影响该列表对象的整个生存周期,例子如下: 

1
2
3
4
5
6
7
def test(a, b):
    c=[]
    d=[]
    c.append(a[:])
    c[0][1] = 'test'
    d.append(b)
    d[0][1] = 'test'
1
2
3
4
5
a=[1,2,3]
b=[4,5,6]
test(a, b)
print a
print b
[1, 2, 3]
[4, 'test', 6]

可见a变了,而b没变

1
2
myDat, labels = createDataSet()
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

1
splitDataSet(myDat,0, 1)
[[1, 'yes'], [1, 'yes'], [0, 'no']]

1
splitDataSet(myDat,0, 0)
[[1, 'no'], [1, 'no']]

选择最好的数据划分方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in xrange(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature
1
chooseBestFeatureToSplit(myDat)
0

1
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

递归构建决策树

多数表决

1
2
3
4
5
6
7
8
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys:
            classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sortd(classCount, key=lambda x: x[1], reversed=True)
    return sortedClassCount[0][0]

创建树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
#     print bestFeat, dataSet
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del labels[bestFeat]
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree
1
2
myDat, labels = createDataSet()
myTree = createTree(myDat, labels)
1
myTree
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

在Python中使用Matplotlib绘制树形图

Matplotlib注解

使用文本注解绘制树节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
    
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, 
                            textcoords='axes fraction', va='center', ha='center', bbox=nodeType,
                           arrowprops=arrow_args)
    
def createPlot():
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    createPlot.ax1 = plt.subplot(111, frameon=False)
    plotNode(u'decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
    plotNode(u'leafnode', (0.8, 0.1), (0.3, 0.8), leafNode)
    plt.show()
1
createPlot()

构造注释解

获取叶节点的数目和树的层数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
#             print numLeafs
        else: numLeafs += 1
    return numLeafs        

def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else : thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

def retrieveTree(i):
    listOfTrees = [{'no surfacing': {0: 'no', 1: {'flippers':{0: 'no', 1: 'yes'}}}},
                   {'no surfacing': {0: 'no', 1: {'flippers':{0: {'head':{0: 'no', 1: 'yes'}}, 1: 'no'}}}}]
    return listOfTrees[i]
1
getNumLeafs(retrieveTree(0))
3

1
getNumLeafs(retrieveTree(1))
4

1
getTreeDepth(retrieveTree(0))
2

1
getTreeDepth(retrieveTree(1))
3

绘制树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#在父子节点间填充文本消息
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString)
    
def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = myTree.keys()[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff -= 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.xOff += 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff += 1.0/plotTree.totalD
    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()
1
createPlot(retrieveTree(0))

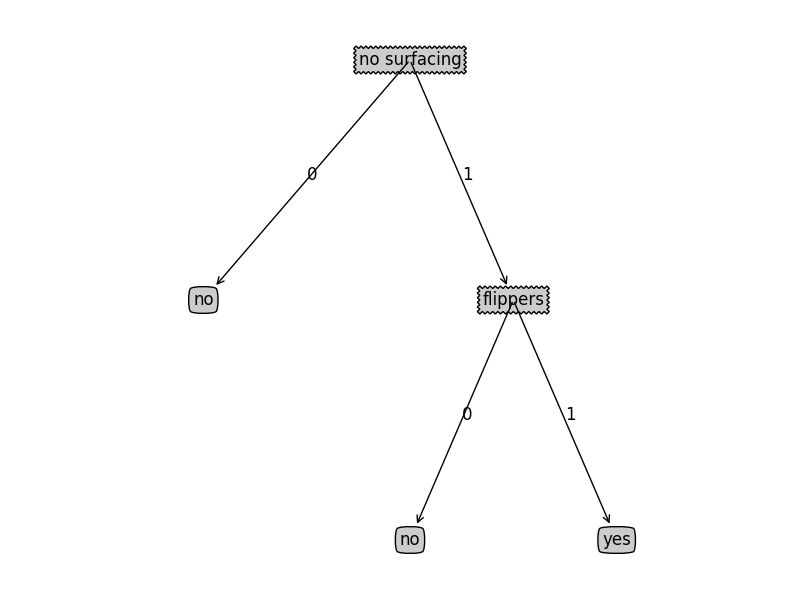
1
createPlot(retrieveTree(1))

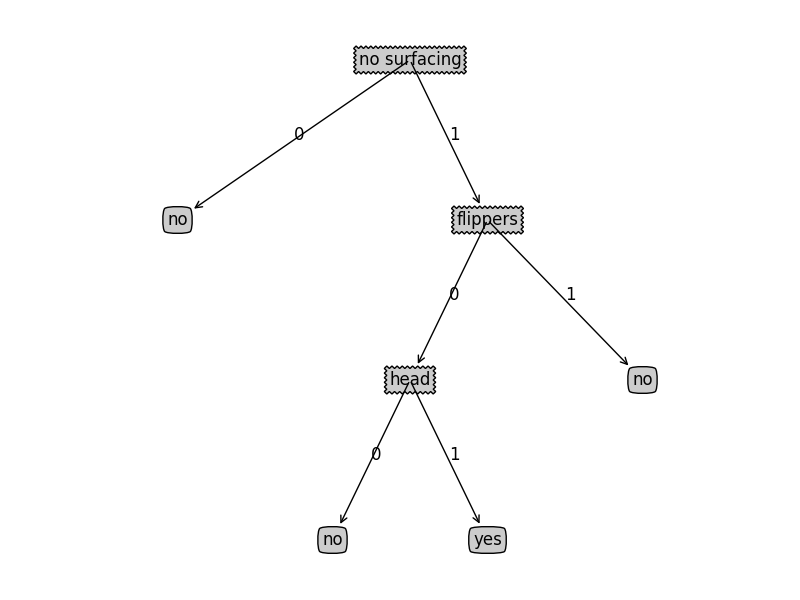
测试和存储分类器

测试算法 : 使用决策树执行分类

1
2
3
4
5
6
7
8
9
10
11
def classify(inputTree, featLabels, testVec):
    firstStr = inputTree.keys()[0]
    secondStr = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    for key in secondStr.keys():
        if testVec[featIndex] == key:
            if type(secondStr[key]).__name__ == 'dict':
                classLabel = classify(secondStr[key], featLabels, testVec)
            else:
                classLabel = secondStr[key]
    return classLabel
1
myDat, labels = createDataSet()
1
myTree = retrieveTree(0)
1
classify(myTree, labels, [1,1])
'yes'

使用算法: 决策树的存储

使用pickle模块存储决策树 

1
2
3
4
5
6
7
8
9
10
def storeTree(inputTree, filename):
    import pickle
    fw = open(filename, 'w')
    pickle.dump(inputTree, fw)
    fw.close

def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)
1
storeTree(myTree, 'test.txt')
1
grabTree('test.txt')
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

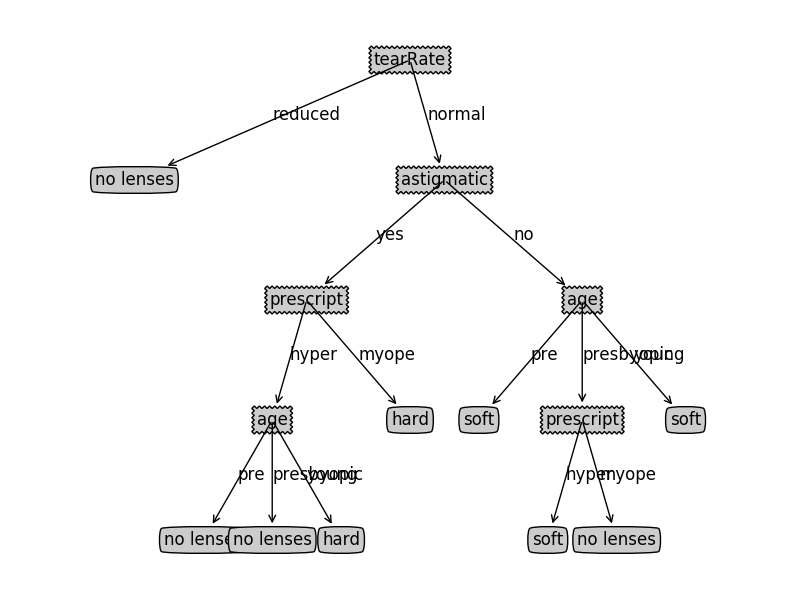
使用决策树预测隐形眼睛类型

1
2
fr = open('lenses.txt')
lenses = [inst.strip().split('\t') for inst in fr.readlines()]
1
2
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
lensesTree = createTree(lenses, lensesLabels)
1
lensesTree
{'tearRate': {'normal': {'astigmatic': {'no': {'age': {'pre': 'soft',
      'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}},
      'young': 'soft'}},
    'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses',
        'presbyopic': 'no lenses',
        'young': 'hard'}},
      'myope': 'hard'}}}},
  'reduced': 'no lenses'}}

1
createPlot(lensesTree)